Using the NumericalGradientIMNN

When we do not have a generative model which we can automatically or analytically calculate the derivatives of some simulations we have to resort to numerical methods to calculate the derivatives of the network outputs with respect to the physical model parameters necessary to fit an IMNN. To do this we will use seed-matched derivatives, i.e. simulations will be made at parameter values above and below the fiducial for each parameter respectively and using the same seed for each variation within the pairs. It is important to use seed matching because this way there is an exact way to separate the effect of realisation from parameters - many more realisations will be needed and fitting will be much more difficult without seed matching. Note that with a fixed data set for training an IMNN it is important to have a validation set for early stopping. This is because, with a limited training set there will be accidental correlations which look like they are due to parameters and the IMNN will extract these features. Using a validation set for early stopping makes sure that once all the features in the validation set have been extracted then no extra information can be incorrectly processed.

For this example we are going to summaries the unknown mean, \(\mu\), and variance, \(\Sigma\), of \(n_{\bf d}=10\) data points of two 1D random Gaussian field, \({\bf d}=\{d_i\sim\mathcal{N}(\mu,\Sigma)|i\in[1, n_{\bf d}]\}\). This is an interesting problem since we know the likelihood analytically, but it is non-Gaussian

\[\mathcal{L}({\bf d}|\mu,\Sigma) = \prod_i^{n_{\bf d}}\frac{1}{\sqrt{2\pi|\Sigma|}}\exp\left[-\frac{1}{2}\frac{(d_i-\mu)^2}{\Sigma}\right]\]

As well as knowing the likelihood for this problem, we also know what sufficient statistics describe the mean and variance of the data - they are the mean and the variance

\[\frac{1}{n_{\bf d}}\sum_i^{n_{\bf d}}d_i = \mu\textrm{ and }\frac{1}{n_{\bf d}-1}\sum_i^{n_{\bf d}}(d_i-\mu)^2=\Sigma\]

What makes this an interesting problem for the IMNN is the fact that the sufficient statistic for the variance is non-linear, i.e. it is a sum of the square of the data, and so linear methods like MOPED would be lossy in terms of information.

We can calculate the Fisher information by taking the negative second derivative of the likelihood taking the expectation by inserting the relations for the sufficient statistics, i.e. and examining at the fiducial parameter values

\[\begin{split}{\bf F}_{\alpha\beta} = -\left.\left(\begin{array}{cc}\displaystyle-\frac{n_{\bf d}}{\Sigma}&0\\0&\displaystyle-\frac{n_{\bf d}}{2\Sigma^2}\end{array}\right)\right|_{\Sigma=\Sigma^{\textrm{fid}}}.\end{split}\]

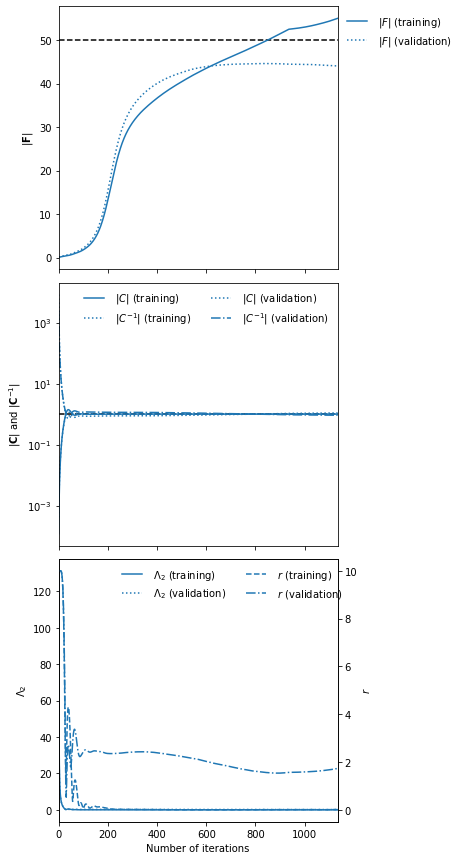
Choosing fiducial parameter values of \(\mu^\textrm{fid}=0\) and \(\Sigma^\textrm{fid}=1\) we find that the determinant of the Fisher information matrix is \(|{\bf F}_{\alpha\beta}|=50\).

from imnn import NumericalGradientIMNN

import jax
import jax.numpy as np
from jax.experimental import stax, optimizers

We’re going to use 1000 summary vectors, with a length of two, at a time to make an estimate of the covariance of network outputs and the derivative of the mean of the network outputs with respect to the two model parameters.

n_s = 1000
n_d = n_s

n_params = 2
n_summaries = n_params

input_shape = (10,)

The simulator is simply

def simulator(key, θ):
    return θ[0] + jax.random.normal(key, shape=input_shape) * np.sqrt(θ[1])

Our fiducial parameter values are \(\mu^\textrm{fid}=0\) and \(\Sigma^\textrm{fid}=1\). We will vary these values by \(\delta\mu=0.1\) and \(\delta\Sigma=0.1\).

θ_fid = np.array([0., 1.])
δθ = np.array([0.1, 0.1])
θ_der = (θ_fid + np.einsum("i,jk->ijk", np.array([-1., 1.]), np.diag(δθ) / 2.)).reshape((-1, 2))

For initialising the neural network a random number generator and we’ll grab another for generating the data:

rng = jax.random.PRNGKey(0)
rng, model_key, data_key = jax.random.split(rng, num=3)

We’ll make the keys for each of the simulations for fitting and validation

data_keys = np.array(jax.random.split(rng, num=2 * n_s))

fiducial = jax.vmap(simulator)(
    data_keys[:n_s],
    np.repeat(np.expand_dims(θ_fid, 0), n_s, axis=0))
validation_fiducial = jax.vmap(simulator)(
    data_keys[n_s:],
    np.repeat(np.expand_dims(θ_fid, 0), n_s, axis=0))
numerical_derivative = jax.vmap(simulator)(
    np.repeat(data_keys[:n_s], θ_der.shape[0], axis=0),
    np.tile(θ_der, (n_s, 1))).reshape(
        (n_s, 2, n_params) + input_shape)
validation_numerical_derivative = jax.vmap(simulator)(
    np.repeat(data_keys[n_s:], θ_der.shape[0], axis=0),
    np.tile(θ_der, (n_s, 1))).reshape(
        (n_s, 2, n_params) + input_shape)

We’re going to use jax’s stax module to build a simple network with three hidden layers each with 128 neurons and which are activated by leaky relu before outputting the two summaries. The optimiser will be a jax Adam optimiser with a step size of 0.001.

model = stax.serial(
    stax.Dense(128),
    stax.LeakyRelu,
    stax.Dense(128),
    stax.LeakyRelu,
    stax.Dense(128),
    stax.LeakyRelu,
    stax.Dense(n_summaries))
optimiser = optimizers.adam(step_size=1e-3)

The NumericalGradientIMNN can now be initialised setting up the network and the fitting routine (as well as the plotting function)

imnn = NumericalGradientIMNN(
    n_s=n_s, n_d=n_d, n_params=n_params, n_summaries=n_summaries,
    input_shape=input_shape, θ_fid=θ_fid, model=model,
    optimiser=optimiser, key_or_state=model_key, δθ=δθ,
    fiducial=fiducial, derivative=numerical_derivative,
    validation_fiducial=validation_fiducial,
    validation_derivative=validation_numerical_derivative)

To set the scale of the regularisation we use a coupling strength \(\lambda\) whose value should mean that the determinant of the difference between the covariance of network outputs and the identity matrix is larger than the expected initial value of the determinant of the Fisher information matrix from the network. How close to the identity matrix the covariance should be is set by \(\epsilon\). These parameters should not be very important, but they will help with convergence time.

λ = 10.
ϵ = 0.1

Fitting can then be done simply by calling:

imnn.fit(λ, ϵ, print_rate=1)

0it [00:00, ?it/s]

Here we have included a print_rate for a progress bar, but leaving this out will massively reduce fitting time (at the expense of not knowing how many iterations have been run). The IMNN is run (by default) for a maximum of max_iterations = 100000 iterations, but with early stopping which can turn on after min_iterations = 100 iterations and after patience = 100 iterations where the maximum determinant of the Fisher information matrix has not increased. imnn.w is set to the values of the network parameters which obtained the highest value of the determinant of the Fisher information matrix, but the values at the final iteration can be set using best = False.

To continue training one can simply rerun fit

imnn.fit(λ, ϵ, print_rate=1)

0it [00:00, ?it/s]

To visualise the fitting history we can plot the results:

imnn.plot(expected_detF=50);